Giải vô địch bóng đá U-23 châu Á năm 2020 đã diễn ra. Ở giải đấu này, nếu thi đấu thành công và lọt được tới trận chung kết, đội tuyển bóng đá U-23 Việt Nam sẽ được thi đấu trên ba sân vận động khác nhau trên đất Thái, đó là sân vận động Buriram (gọi là sân vận động 1), sân vận động Rajamangala (sân vận động 2), và sân vận động Thamasat (sân vận động 3).

Để thuận tiện cho việc bình luận các trận đấu, đài truyền hình VTV muốn một điểm tập kết thỏa mãn các điều kiện sau:

Điều kiện 1: Góc trông từ điểm đó giữa ba sân vận động phải bằng nhau. Góc trông \theta từ một điểm A đến một sân vận động có dạng hình tròn tâm O bán kính r được tính bằng công thức \theta = 2 \arctan\frac{r}{OA}

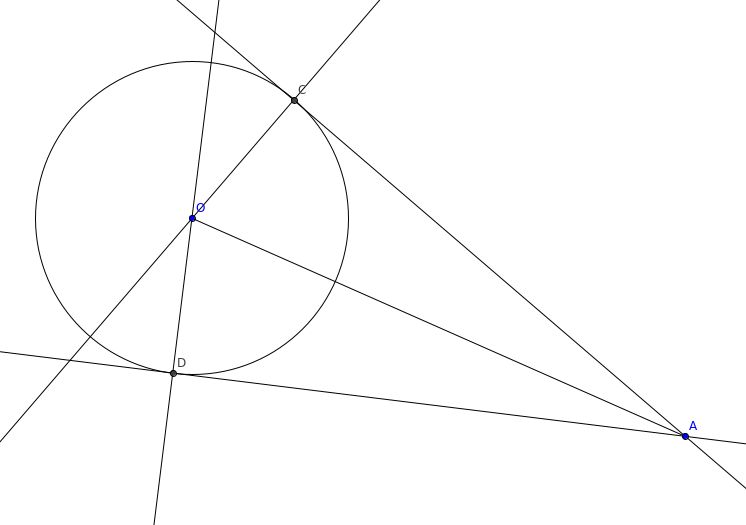
Trong hình trên, góc trông từ điểm A đến sân vận động bằng số đo của \angle CAD . Lưu ý rằng việc các sân vận động có thể chắn nhau không ảnh hưởng đến giá trị của góc trông.

Điều kiện 2: Góc trông này phải lớn nhất có thể.

Hãy giúp đài truyền hình VTV tìm điểm tập kết thỏa mãn các điều kiện trên.

• Dòng đầu tiên gồm ba số nguyên x_1, y_1, r_1 mô tả sân vận động Buriram có tâm (x_1, y_1) và bán kính r_1.
• Dòng thứ hai gồm ba số nguyên x_2, y_2, r_2 mô tả sân vận động Rajamangala có tâm (x_2, y_2) và bán kính r_2.
• Dòng thứ ba gồm ba số nguyên x_3, y_3, r_3 mô tả sân vận động Thamasat có tâm (x_3, y_3) và bán kính r_3.

Dữ liệu vào đảm bảo -10^3 \leq x_i, y_i \leq 10^3, 1 \leq r_i \leq 10^3, các hình tròn biểu diễn các sân vận động không có điểm chung nào, và tâm ba sân vận động không thẳng hàng.

Nếu tồn tại điểm tập kết thỏa mãn yêu cầu bài toán, in ra hai số thực lần lượt là hoành độ và tung độ của điểm đó (Làm tròn 5 chữ số sau phần thập phân). Nếu không tồn tại điểm nào thỏa mãn điều kiện 1, in ra -1.